LINEAR LEAST SQUARES FIT MAPPING METHOD FOR INFORMATION
RETRIEVAL FROM NATURAL LANGUAGE TEXTS
ABSTRACT
This paper describes a unique method for mapping natural
language texts to canonical terms that identify the
contents of the texts. This method learns empirical associations
between free-form texts and canonical terms
from human-assigned matches and determines a Linear
Least Squares Fit (LLSF) mapping function which
represents weighted connections between words in the
texts and the canonical terms. The mapping function
enables us to project an arbitrary text to the canonical
term space where the "transformed" text is compared
with the terms, and similarity scores are obtained
which quantify the relevance between the the text and
the terms. This approach has superior power to discover
synonyms or related terms and to preserve the
context sensitivity of the mapping. We achieved a rate
of 84% in both the recall and the precision with a testing
set of 6,913 texts, outperforming other techniques
including string matching (15%), morphological parsing
(17%) and statistical weighting (21%).
1. Introduction
A common need in natural language information retrieval
is to identify the information in free-form texts
using a selected set of canonical terms, so that the texts
can be retrieved by conventional database techniques
using these terms as keywords. In medical classification,
for example, original diagnoses written by physicians
in patient records need to be classified into canonical
disease categories which are specified for the purposes
of research, quality improvement, or billing. We
will use medical examples for discussion although our
method is not limited to medical applications.
String matching is a straightforward solution to automatic
mapping from texts to canonical terms. Here we
use "term" to mean a canonical description of a concept,
which is often a noun phrase. Given a text (a
"query ") and a set of canonical terms, string matching
counts the common words or phrases in the text and
the terms, and chooses the term containing the largest
overlap as most relevant. Although it is a simple and
therefore widely used technique, a poor success rate
(typically 15% - 20%) is observed [1]. String-matching-based
methods suffer from the problems known as "too
little" and "too many". As an example of the former,
high blood pressure and hypertension are synonyms but
a straightforward string matching cannot capture the
equivalence in meaning because there is no common
word in these two expressions. On the other hand, there
are many terms which do share some words with the
query high blood pressure, such as high head at term,
fetal blood loss, etc.; these terms would be found by a
string matcher although they are conceptually distant
from the query,
Human-defined synonyms or terminology thesauri have
been tried as a semantic solution for the "too little"
problem [2] [3]. It may significantly improve the mapping
if the right set of synonyms or thesaurus is available.
However, as Salton pointed out [4], there is "no
guarantee that a thesaurus tailored to a particular text
collection can be usefully adapted to another collection.
As a result, it has not been possible to obtain
reliable improvements in retrieval effectiveness by using
thesauruses with a variety of different document
collections".
Salton has addressed the problem from a different angle,
using statistics of word frequencies in a corpus to estimate
word importance and reduce the "too many" irrelevant
terms [5]. The idea is that "meaningful" words
should count more in the mapping while unimportant
words should count less. Although word counting is
technically simple and this idea is commonly used in
existing information retrieval systems, it inherits the
basic weakness of surface string matching. That is,
words used in queries but not occurring in the term collection
have no affect on the mapping, even if they are
synonyms of important concepts in the term collection.
Besides, these word weights are determined regardless
of the contexts where words have been used, so the lack
of sentitivity to contexts is another weakness.
We focus our efforts on an algorithmic solution for achieving
the functionality of terminology thesauri and semantic
weights without requiring human effort in identifying
synonyms. We seek to capture such knowledge
through samples representing its usage in various contexts,
e.g. diagnosis texts with expert-assigned canonical
terms collected from the Mayo Clinic patient record
archive. We propose a numerical method, a "Linear
Least Squares Fit" mapping model, which enables us
to obtain mapping functions based on the large collection
of known matches and then use these functions to
determine the relevant canonical terms for an arbitrary
text.
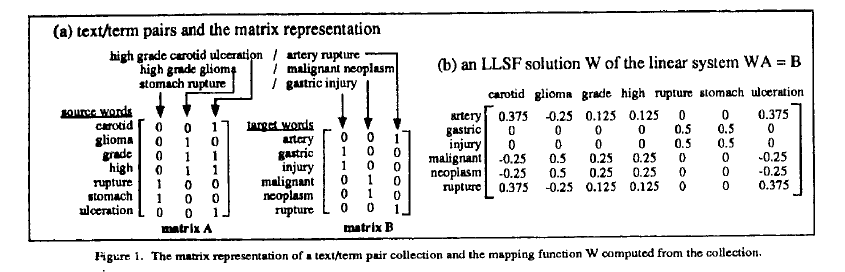
2. Computing an LLSF mapping function
We consider a mapping between two languages, i.e.
from a set of texts to a set of canonical terms. We
call the former the source language and the latter the
target language. For convenience we refer to an item
in the source language (a diagnosis) as "text", and an
item in the target language (a canonical description of
a disease category) as "canonical term" or "term". We
use "text" or "term" in a loose sense, in that it may be
a paragraph, a sentence, one or more phrases, or simply
a word. Since we do not restrict the syntax, there is no
difference between a text and a term, both of them are
treated as a set of words.
2.1 A numerical representation of texts
In mathematics, there are well-established numerical
methods to approximate unknown functions using known
data. Applying this idea to our text-to-term mapping,
the known data are text/term pairs and the unknown
function we want to determine is a correct (or nearly
correct) text-to-term mapping for not only the texts included
in the given pairs, but also for the texts which
are not included. We need a numerical representation
for such a computation.
Vectors and matrices have been used for representing
natural language texts in information retrieval systems
for decades [5]. We employ such a representation in
our model as shown in Figure 1 (a). Matrix A is a
set of texts, matrix B is a set of terms, each column
in A represents an individual text and the corresponding
column of B represents the matched term. Rows
in these matrices correspond to words and cells contain
the numbers of times words occur in corresponding
texts or terms.
2.2 The mapping function
Having matrix .A and B, we are ready to compute the
mapping function by solving the equation WA = B
where W is the unknown function. The solution W, if
it exists, should satisfy all the given text/term pairs,
i.e. the equation 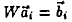 holds for i = 1, ...,k,
where holds for i = 1, ...,k,
where
k is the number of text/term pairs, 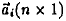 is a
text is a
text
vector, a column of 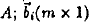 is a term vector, the is a term vector, the
corresponding column in B; n is the number of distinct
source words and m is the number of distinct target
words.
Solving WA = B can be straightforward using techniques
of solving linear equations if the system is consistent.
Unfortunately the linear system WA = B does
not always have a solution because there are only m x n
unknowns in W, but the number of given vector pairs
may be arbitrarily large and form an inconsistent system.
The problem therefore needs to be modified as a
Linear Least Squares Fit which always has at least one
solution.
Definition 1. The LLSF problem is to find W which
minimizes the sum
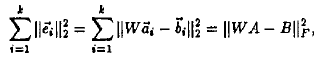
where 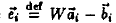 is the mapping error of the ith is the mapping error of the ith
text/term pair; the notation 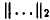 is vector
2-norm, is vector
2-norm,
defined as 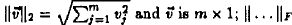 is is
the Frobenius matrix norm, defined as
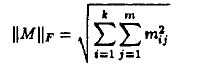
and M is m x k.
The meaning of the LLSF problem is to find the mapping
function W that minimizes the total mapping errors
for a given text/term pair collection (the "training
set"). The underlying semantics of the transformation
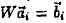 is to "translate" the meaning of each source is to "translate" the meaning of each source
word in the text into a set of target words with weights,
and then linearly combine the translations of individual
words to obtain the translation of the whole text,
Figure 1 (b) is the W obtained from matrix A and B
in (a). The columns of W correspond to source words,
the rows correspond to target words, and the ceils are
the weights of word-to-word connections between the
two languages. A little algebra will show that vector
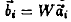 is the sum of the column vectors in W, which is the sum of the column vectors in W, which
correspond to the source words in the text.
The weights in W are optimally determined according
to the training set. Note that the weights do not depend
on the literal meanings of words. For example, the
source word glioma has positive connections of 0.5 to
both the target words malignant and neoplasm, showing
that these different words are related to a certain
degree. On the other hand, rupture is a word shared by
both the source language and the target language, but
the source word rupture and the target word rupture
have a connection weight of 0 because the two words
do not co-occur in any of the text/term pairs in the
training set. Negative weight is also possible for words
that do not co-occur and its function is to preserve the
context sensitivity of the mapping. For example, high
grade in the context of high grade carotid ulceration
does not lead to a match with malignant neoplasm,
as it would if it were used in the context high grade
glioma, because this ambiguity is cancelled by the negative
weights. Readers can easily verify this by adding
the corresponding column vectors of W for these two
different contexts.
2.3 The computation
A conventional method for solving the LLSF is to use
singular value decomposition (SVD) [6] [7]. Since mathematics
is not the focus of this paper, we simply outline
the computation without proof.
Given matrix A (n x k) and B (mx k), the computation
of an LLSF for WA = B consists of the following steps:
(1) Compute an SVD of A, yielding matrices U, S and
V:
if 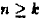 , decompose A such that , decompose A such that
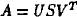 , ,
if n < k, decompose the transpose AT such that
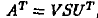
where U (n x p) sad V (k x p) contain the left and
right singular vectors, respectively, and 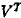 is is
the transpose of V; Sis a diagonal (pxp) which
contains p non-zero singular values 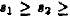
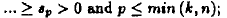
(2) Compute the mapping function
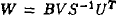
where 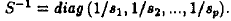
3, Mapping arbitrary queries to canonical terms
The LLSF mapping consists of the following steps:
(1) Given an arbitrary text (a "query"), first form a
query vector,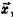 in the source vector space. in the source vector space.
A query vector is similar to a colunm of matrix A, whose
elements contain the numbers of times source words
occur in the query. A query may Mso contain some
words which are not in the source language; we ignore
these words because no meaningful connections with
them are provided by the mapping function. As an
example, query severe stomach ulcers*ion is converted
into vector 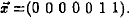
(2) Transform the source vector
 into into  in
the in
the
target space.
In our example, 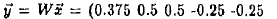
0.375). Differing from text vectors in A and term vectors
in B, the elements (coefficients) of 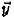 are not
limited are not
limited
to non-negative integers. These numbers show how the
meaning of a query distributes over the words in the
target language.
(3) Compare query-term similarity for all the term vectors
and find the relevant terms.
In linear algebra, cosine-theta (or dot-product) is a
common measure for obtaining vector similarity. It is
also widely accepted by the information retrieval community
using vector-based techniques because of the
reasonable underlying intuition: it captures the similarity
of texts by counting the similarity of individual
words and then summarizing them. We use the cosine
value to evaluate query-term similarity, defined as below;
Definition 2. Let 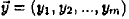 be
the query vector be
the query vector
in the target space and 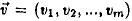 be a term be a term
vector in the target space,
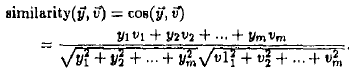
In order to find the closest match, we need to compare
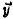 with all the term vectors. We use C to
denote the with all the term vectors. We use C to
denote the
matrix of these vectors distinct from matrix B which
represents the term collection in the training set. In
general only a subset of terms are contained in a training
set, so (7 has more columns than the unique columns
of B. Furthermore, C could have more rows than B because
of the larger vocabulary. However, since only the
words in B have meaningful connections in the LLSF
mapping function, we use the words in B to form a reduced
target language and trim C into the same rows
as B. Words not in the reduced target language are
ignored.
An exhaustive comparison of the query-term similarity
values provides a ranked list of all the terms with respect
to a query. A retrieval threshold can be chosen for
drawing a line between relevant and irrelevant. Since
relevance is often a relative concept, the choice of the
threshold is left to the application or experiment.
A potential weakness of this method is that the term
vectors in matrix C are all surface-based (representing
word occurrence frequency only) and are not affected
by the training set or the mapping function. This weakness
can be attenuated by a refined mapping method
using a reverse mapping function R which is an LLSF
solution of the linear system RB = A. The refinement
is described in a separate paper [8].
4. The results
4.1 The primary test
We tested our method with texts collected from patient
records of Mayo Clinic. The patient records include diagnoses
(DXs) written by physicians, operative reports
written by surgeons, etc. The original texts need to be
classified into canonical categories and about 1.5 million
patient records are coded by human experts each
year. We arbitrarily chose the cardiovascular disease
subset from the 1990 surgical records for our primary
test. After human editing to separate these texts from
irrelevant parts in the patient records and to clarify the
one-to-one correspondence between DXs and canonical
terms, we obtained a set of 6,913 DX/term pairs. The
target language consists of 376 canonical names of cardiovascular
diseases as defined in the classification system
ICD-9-CM [9]. A simple preproceseing was applied
to remove punctuation and numbers, but no stemming
or removal of non-discriminative words were used.
We split the 6,913 DXs into two halves, called "oddhalf"
and "even-half". The odd-half was used as the
training set, the even-half was used as queries, and the
expert-assigned canonical terms of the even-half were
used to evaluate the effectiveness of the LLSF mapping.
We used conventional measures in the evaluation: recall
and precision, defined as

For the query set of the even-half, we had a recall rate
of 84% when the top choice only was counted and 96%
recall among the top five choices. We also tested the
odd-half, i.e. the training set itself, as queries and had
a recall of 92% with the top choice and 99% with the
top five. In our testing set, each text has one and only
one relevant (or correct) canonical term, so the recall is
always the same as the precision at the top choice.
Our experimental system is implemented as a combination
of C++, Perl and UNIX shell programming.For SVD, currently we use a matrix
library in C++
[10] which implements the same algorithm as in LINPACK[
Ill. A test with 3,457 pairs in the training set
took about 4.45 hours on a SUN SPARCstation 2 to
compute the mapping function W and R. Since the
computation of the mapping function is only needed
once until the data collection is renewed, a real time response
is not required. Term retrieval took 0.45 sec or
less per query and was satisfactory for practical needs.
Two person-days of human editing were needed for preparing
the testing set of the 6,913 DXs.
4.2 The comparison
For comparing our method with other approaches, we
did additional tests with the same query set, the evenhalf
(3,456 DXs), and matched it against the same term
set, the 376 ICD-9-CM disease categories.
For the test of a string matching method, we formed one
matrix for all the 3,456 texts and the 376 terms, and
used the cosine measure for computing the similarities.
Only a 15% recall and precision rate was obtained at
the top choice threshold.
For testing the effect of linguistic canonicalization, we
employed a morphological parser developed by the Evans
group at CMU [12] (and refined by our group by adding
synonyms) which covers over 10,000 lexical variants.
We used it as a preprocessor which converted lexical
variants to word roots, expanded abbreviations to full
spellings, recognized non-discriminative categories such
as conjunctions and prepositions and removed them,
and converted synonyms into canonical terms. Both the
texts and the terms were parsed, and then the string
matching as mentioned above was applied. The recall
(and precision) rate was 17% (i.e. only 2% improvement),
indicating that lexical canonicalization does not
solve the crucial part of the problem; obviously, very
little information was captured. Although synonyms
were also used, they were a small collection and not
especially favorable for the cardiovascular diseases.
For testing the effectiveness of statistical weighting, we
ran the SMART system (version 10) developed at Cornell
by Salton's group on our testing set. Two weighting
schemes, one using term frequency and another using a
combination of term frequency and "inverse document
frequency", were tested with default parameters; 20%
and 21% recall rates (top choice) were obtained, respectively.
An interactive scheme using user feedback
for improvement is also provided in SMART, but our
tests did not include that option.
For further analysis we checked the vocabulary overlap
between the query set and the term set. Only 20%
of the source words were covered by the target words,
which partly explains the unsatisfactory results of the
above methods. Since they are all surface-based upproaches,
only 20% of the query words were effectively
used and roughly 80% of the information was ignored.
There approaches share a common weakness in that
they can not capture the implicit meaning of words (or
only captured a little), and this seems to be a crucial
problem.
Table l. The test summary of different methods
| Method |
recall of the top choice |
recall of top five choices |
| string matching |
15% |
42% |
| sring matching enhanced by a morphological
psrsing |
17% |
46% |
| SMART: staristical weighting using IDF |
21% |
48% |
| LLSF: training act = odd-half |
84% |
96% |
| LLSF: training met = odd-half, query set =
odd-half |
92% |
99% |
(1) The "even-half" (3,456 DXs) was used as the query set
for testis 8 all the methods above, except the last one;
(2) the "odd-half' (3,457 DXs) was used as the training set in the LLSF tests,
which formed a source language including
945 distinct words and t lascar language (reduced) including 376 unique
canonical terms and 224 distinct words;
3) the refined mapping method mentioned in Section 3 was used in the LLSF tests.

The LLSF method, on the other hand, does not have
such disadvantages. First, since the training set and
the query set were from the same data collection, a
much higher vocabulary coverage of 67% was obtained.
Second, the 67% source words were further connected
to their synonyms or related words by the LLSF mapping,
according to the matches in the training set. Not
only word co-occurrence, "but also the contexts (sets of
words) where the words have been used, were taken into
account in the computation of weights; these connections
were therefore context-sensitive. As a result, the
67% word coverage achieved an 84% recall and precision
rate (top choice), outperforming the other methods
by 63% or more. Table 1 summarizes these tests.
Figure 2 shows some sample results where each query is
listed with the top choice by the LLSF mapping and the
top choice by the string matching. All the terms chosen
by the LLSF mapping agreed with expert-assigned
matches. It is evident that the LLSF mapping successfully
captures the semantic associations between the
different surface expressions where as the string matching
failed completely or missed important information.
5. Discussion
5.1 Impact to computational linguistics
Recognizing word meanings or underlying concepts in
natural language texts is a major focus in computational
linguistics, especially in applied natural language
processing such as information retrieval. Lexico-syntaetic
approaches have had limited achievement because lexical
canonicalization and syntactic categorization can
not capture much information about the implicit meaning
of words and surface expressions. Knowledge-based
approaches using semantic thesauri or networks, on the
other hand, lead to the fundamental question about
what should be put in a knowledge base. Is a general
knowledge base for unrestricted subject areas realistic?
If unlikely, then what should be chosen for a
domain-specific or application-specific knowledge bane?
Is there a systematic way to avoid ad hoe decisions or
the inconsistency that have often been involved in human
development of semantic classes and the relationships
between them? No clear answers have been given
for these questions.
The LLSF method gives an effective solution for capturing
semantic implications between surface expressions.
The word-to-word connections between two languages
capture synonyms and related terms with respect to the
contexts given in the text/term pairs of the training set.
Furthermore, by taking a training set from the same
data collection as the queries the knowledge (semantics)
is self-restricted, i.e. domain-specific, application-specific
and user-group-specific. No symbolic representation
of the knowledge is involved nor necessary, so
subjective decisions by humans are avoided. As a result,
the 6%69% improvement over the string matching
and the morphological parsing is evidence of our assertions.
5.2 Difference from other vector-based methods
The use of vector/matrix representation, cosine measure
and SVD makes our approach look similar to other
vector-based methods, e.g. Saiton's statistical weighting
scheme and Deerwester's Latent Semantic Indexing
(LSI) [13] which uses a word-document matrix and
truncated SVD technique to adjust word weights in a
document retrieval. However, there is a fundamental
difference in that they focus on word weights based on
counting word occurrence frequencies in a text collection,
so only the words that appeared in queries and
documents (terms in our context) have an affect on the
retrieval. On the other hand, we focus on the weights
of word-to-word connections between two languages,
not weight of words; our computation is based on the
information of human-assigned matches, the word cooccurrence
and the contexts in the text/term pairs, not
simply word occurrence frequencies. Our approach has
an advantage in capturing synonyms or terms semantically
related at various degrees and this makes a significant
difference. As we discussed above, only 20% of
query words were covered by the target words. So even
if the statistical methods could find optimal weights for
these words, the majority of the information was still
ignored, and as a result, the top choice recall and precision
rate of SMART did not exceed 20% by much. Our
tests with the LSI were mentioned in a separate paper
[14]; the results were not better than SMART or the
string matching method discussed above.
In short, besides the surface characteristics such as
using
matrix, cosine-theta and SVD, the LLSF mapping
uses different information and solves the problem on a
different scale.
5.3 Potential applications
We have demonstrated the success of the LLSF mapping
in medical classification, but our method is not
limited to this application. An attractive and practical
application is automatic indexing of text databases
and a retrieval using these indexing terms. As most
existing text databases use human-assigned keywords
for indexing documents, numerous amounts of document/
term pairs can be easily collected and used as
training sets. The obtained LLSF mapping functions
then can be used for automatic document indexing with
or without human monitoring and refinement. Queries
for retrieval can be mapped to the indexing terms using
the same mapping functions and the rest of the task is
simply a keyword-based search.
Another interesting potential is machine translation.
Brown[15] proposed a statistical approach for machine
translation which used word-to-word translation probability
between two languages. They had about three
million pairs of English-French sentences but the difficult
problem was to break the sentence-to-sentence
association down to word-to-word. While they had
a sophisticated algorithm to determine an alignment
of word connections with maximum probability, it required
estimation and re-estimation about possible alignments.
Our LLSF mapping appears to have a great opportunity
to discover the optimal word-to-word translation
probability, according to the English-French sentence
pairs but without requiring any subjective estimations.
5.4 Other aspects
Several questions deserve a short discussion: is the word
a good choice for the basis of the LLSF vector space?
Is the LLSF the only choice or the best choice for a
numerical mapping?
The word is not the only choice as the basis. We use it
as a suitable starting point and for computational efficiency.
We also treat some special phrases such as Acquired
Immunodeficiency Syndrome as a single word, by
putting hyphens between the words in a pre-formatting.
An alternative choice to using words is to use noun
phrases for invoking more syntactic constraints. While
it may improve the precision of the mapping (how much
is unclear), a combinatorial increase of the problem size
is the trade-off.
Linear fit is a theoretical limitation of the LLSF mapping
method. More powerful mapping functions are
used in some neural networks[16]. However, the fact
that the LLSF mapping is simple, fast to compute,
and has well known mathematical properties makes it
preferable at this stage of research. There are other numerical
methods possible, e.g. using polynomial fit instead
of linear fit, or using interpolation (going through
points) instead of least squares fit, etc. The LLSF
model demonstrated the power of numerical extraction
of the knowledge from human-assigned mapping
results, and finding the optimal solution among different
fitting methods is a matter of implementation and
Acknowledgement
We would like to thank Tony Plate and Kent Bailey
for fruitful discussions and Geoffrey Atkin for programruing.
|



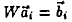 holds for i = 1, ...,k,
where
holds for i = 1, ...,k,
where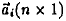 is a
text
is a
text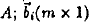 is a term vector, the
is a term vector, the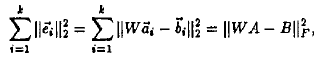
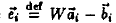 is the mapping error of the ith
is the mapping error of the ith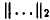 is vector
2-norm,
is vector
2-norm,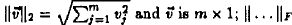 is
is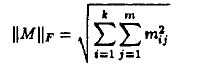
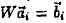 is to "translate" the meaning of each source
is to "translate" the meaning of each source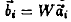 is the sum of the column vectors in W, which
is the sum of the column vectors in W, which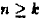 , decompose A such that
, decompose A such that
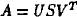 ,
,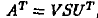
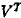 is
is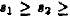
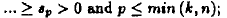
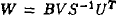
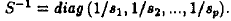
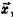 in the source vector space.
in the source vector space.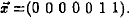
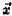 into
into 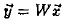 in
the
in
the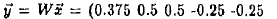
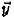 are not
limited
are not
limited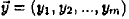 be
the query vector
be
the query vector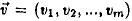 be a term
be a term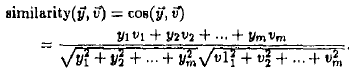
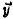 with all the term vectors. We use C to
denote the
with all the term vectors. We use C to
denote the
