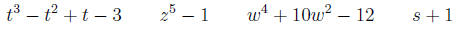|
Home Graphing and Writing Linear Functions SOLVING EQUATIONS INVOLVING RATIONAL EXPONENTS Linear Equations and Graphing Systems of Linear Equations Solving Polynomial Equations Matrix Equations and Solving Systems of Linear Equations Introduction Part II and Solving Equations Linear Algebra Graphing Linear Inequalities Using Augmented Matrices to Solve Systems of Linear Equations Solving Linear Inequalities Solution of the Equations Linear Equations Annotated Bibliography of Linear Algebra Books Write Linear Equations in Standard Form Graphing Linear Inequalities Introduction to Linear Algebra for Engineers Solving Quadratic Equations THE HISTORY OF SOLVING QUADRATIC EQUATIONS Systems of Linear Equations Review for First Order Differential Equations Systems of Nonlinear Equations & their solutions LINEAR LEAST SQUARES FIT MAPPING METHOD FOR INFORMATION RETRIEVAL FROM NATURAL LANGUAGE TEXTS Quadratic Equations Syllabus for Differential Equations and Linear Alg Linear Equations and Matrices Solving Linear Equations Slope-intercept form of the equation Linear Equations DETAILED SOLUTIONS AND CONCEPTS QUADRATIC EQUATIONS Linear Equation Problems Systems of Differential Equations Linear Algebra Syllabus Quadratic Equations and Problem Solving LinearEquations The Slope-Intercept Form of the Equation Final Exam for Matrices and Linear Equations Linear Equations |
Solving Polynomial EquationsIntroductionLinear and quadratic equations, dealt within Sections 3.1 and 3.2, are
members of a class of equations,
in which x is a variable and
PrerequisitesBefore starting this Section you should . . . • be able to solve linear and quadratic Learning OutcomesOn completion you should be able to . . . • recognise and solve some polynomial 1. Multiplying polynomials togetherKey Point 7 A polynomial expression is one of the form
where
For example x3 −17x2 +54x−8 is a polynomial expression in x. The polynomial
may be expressed
Note that only non-negative whole number powers of the variable (usually x)
are allowed in a polynomial The degree of a polynomial is the highest power to which the variable is
raised. Thus x3 + 6x + 2 Let us consider what happens when two polynomials are multiplied together. For example (x + 1)(3x − 2) is the product of two first degree polynomials. Expanding the brackets we obtain (x + 1)(3x − 2) = 3x2 + x − 2 which is a second degree polynomial. In general we can regard a second degree polynomial, or quadratic, as the
product of two first degree (x − 1)(x2 + 3x − 7) = x3 + 2x2 − 10x + 7 is a third degree, or cubic, polynomial which is thus the product of a linear
polynomial and a quadratic In general we can regard a cubic polynomial as the product of a linear
polynomial and a quadratic Key Point 8 A cubic expression can always be formulated as a linear expression times a quadratic expression. If x3 − 17x2 + 54x − 8 = (x − 4) × (a polynomial), state the degree of the Your solution Answer (a) If 3x2 + 13x + 4 = (x + 4) × (a polynomial), state the degree of the (b) What is the coefficient of x in this unknown polynomial ? Your solution (a) (b) Answer (b) It must be 3 in order to generate the term 3x2 when the brackets are removed. If 2x2 + 5x + 2 = (x + 2)× (a polynomial), what must be the coefficient of x
in Your solution Answer Two quadratic polynomials are multiplied together. What is the degree of the Your solution Answer 2. Factorising polynomials and equating coefficientsWe will consider how we might find the solution to some simple polynomial
equations. An important Example 23 Factorise the expression x3−17x2+54x−8 given that one of the factors is (x−4). Solution Given that x − 4 is a factor we can write The polynomial must be quadratic because the expression on the left is cubic
and x − 4 is linear. x3 − 17x2 + 54x − 8 = (x − 4)(ax2 + bx + c) Removing the brackets on the right and collecting like terms together we have Like terms are those which involve the same power of the variable (x). Equating coefficients means that we compare the coefficients of each term on
the left with the As a check we look at the coefficient of x to ensure it is the same on both
sides. Now that we know x3 − 17x2 + 54x − 8 = (x − 4)(x2 − 13x + 2) Exercises Factorise into a quadratic and linear product the given polynomial
expressions Answers 1. (x − 1)(x2 − 5x + 6), 2. (x + 2)(x2 − 2x − 3), 3. (x + 1)(2x2 + 5x + 2), |


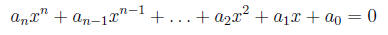
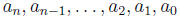 are given constants. Also n must be a positive
are given constants. Also n must be a positive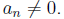 Examples include
Examples include
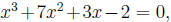
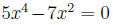 and
and
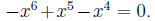

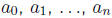 are known coefficients (numbers),
are known coefficients (numbers),
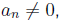 and x is a variable.
and x is a variable.